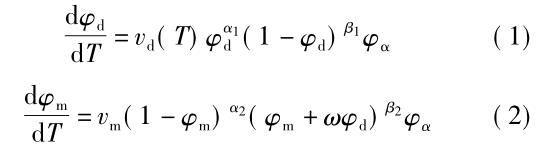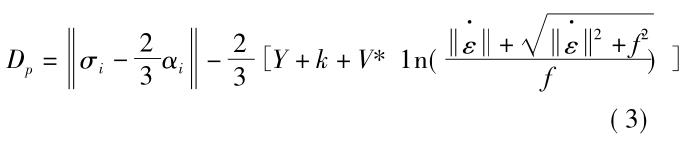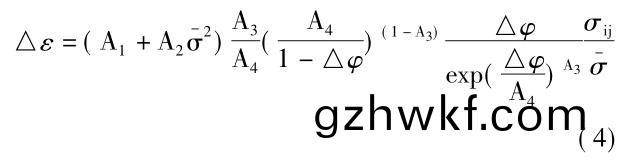热处(chu)理(li)工艺(yi)是实(shi)现零部件(jian)微(wei)观组织(zhi)与性(xing)能调(diao)控的关(guan)键环节��。热处理本(ben)身(shen)是温度(du)、组织(zhi)转(zhuan)变(bian)与(yu)应(ying)力等交互(hu)作用(yong)的复(fu)杂(za)过程(cheng)[1 - 8]���。因此(ci)在(zai)热处(chu)理(li)工(gong)艺(yi)实(shi)践(jian)中(zhong),除微(wei)观(guan)组(zu)织与(yu)性(xing)能的变(bian)外(wai)化(hua),由(you)于温度(du)场(chang)、结(jie)构(gou)等因素的(de)影响(xiang),热处理过(guo)程还会导(dao)致(zhi)残余(yu)应力与(yu)翘曲(qu)变(bian)形��,对(dui)后续(xu)的(de)机加和(he)装配(pei)过程(cheng)带来(lai)不利(li)影响(xiang)[6]���。由于热处理(li)过(guo)程(cheng)受到多个(ge)因素(su)的交互影响(xiang),在实(shi)践中(zhong)很(hen)难通过物(wu)理模(mo)拟的方(fang)式进行(xing)研(yan)究(jiu),特别(bie)是热处(chu)理发生(sheng)在高温(wen)阶(jie)段,无(wu)法(fa)对(dui)组(zu)织、应力(li)�、变(bian)形(xing)等(deng)过(guo)程(cheng)进行(xing)实(shi)时(shi)测(ce)量,室温状(zhuang)态(tai)的(de)分(fen)析(xi)测试(shi)结(jie)果很(hen)难(nan)得到(dao)规律(lv)性成(cheng)果����。因(yin)此采(cai)用仿真技(ji)术(shu)对热(re)处(chu)理(li)过程(cheng)进(jin)行(xing)虚(xu)拟(ni)分(fen)析(xi)�����,对(dui)深入理解(jie)热(re)处理(li)过程的(de)组(zu)织(zhi)���、应力与(yu)温(wen)度(du)之(zhi)间的相互(hu)影(ying)响(xiang)规律,指导工艺设计(ji)具有重要(yao)意义���。
钛(tai)合(he)金广泛应(ying)用(yong)于航(hang)空(kong)����、航(hang)天(tian)等(deng)对零(ling)件(jian)性能和精度(du)要求(qiu)高的领(ling)域,其热处理工(gong)艺设(she)计同样(yang)面(mian)临着(zhe)组(zu)织(zhi)性(xing)能调控����、残(can)余应(ying)力(li)与(yu)变(bian)形(xing)控(kong)制等难(nan)题。近二(er)十年(nian)来(lai)��,在钛(tai)合(he)金(jin)领(ling)域�����,研(yan)究者们在(zai)热(re)处(chu)理相(xiang)变(bian)基础理(li)论�����、数(shu)值模(mo)型(xing)与软(ruan)件(jian)开(kai)发(fa)等方(fang)面开(kai)展了(le)大量研究工作,热处(chu)理工(gong)艺仿真(zhen)在(zai)固(gu)溶时(shi)效�����、退(tui)火、热(re)校(xiao)形等方(fang)面得(de)到了(le)深入应用,有(you)助(zhu)于深入理解(jie)钛合(he)金(jin)零(ling)部(bu)件工(gong)艺(yi)-组织(zhi)-性能的关(guan)联性(xing)�、残(can)余(yu)应(ying)力与变(bian)形间产生(sheng)制(zhi)约机(ji)制,对(dui)热处(chu)理工(gong)艺(yi)优(you)化(hua)设计(ji)起(qi)到了很(hen)好地(di)支(zhi)撑作(zuo)用����。本文(wen)对钛(tai)合(he)金热处(chu)理(li)工(gong)艺(yi)仿(fang)真(zhen)基(ji)础理论(lun)与应用等(deng)方面(mian)展开(kai)综(zong)述,并对未来(lai)的(de)研(yan)究与(yu)应用方向提(ti)出展(zhan)望���,为钛(tai)合金热处(chu)理(li)仿真在相关制造(zao)领(ling)域的(de)应用提(ti)供参考(kao)�。
1�、热处理仿(fang)真基(ji)础(chu)理(li)论与模(mo)型进(jin)展(zhan)
钛合金(jin)的(de)热(re)处(chu)理过(guo)程包含温度�、组织转变(bian)与应(ying)力三(san)方(fang)面交(jiao)互作(zuo)用�����,最(zui)关键环(huan)节是(shi)针对(dui)相变和(he)应(ying)力(li)的(de)数值模(mo)型(xing)�����。因此(ci)����,目前大部(bu)分(fen)基础(chu)理论(lun)与建(jian)模的(de)进展(zhan)主要(yao)集中在这两(liang)方(fang)面(mian)�����。
钛合金(jin)在热(re)处理(li)过程中(zhong)存在(zai)多(duo)种(zhong)类(lei)型的(de)相变(bian)����,其(qi)中 β��、α 相(xiang)之(zhi)间(jian)的(de)转(zhuan)变是(shi)最基(ji)本��、最(zui)重要的一种(zhong),几(ji)乎(hu)所有钛(tai)合金在(zai)高温(wen)冷却(que)或者(zhe)时效过(guo)程中均会发(fa)生�。钛(tai)合(he)金(jin)的 β 相为体(ti)心立方结(jie)构(gou)��,而(er) α 相为密(mi)排(pai)立方(fang) 结 构(gou),两 相(xiang) 之 间 存(cun) 在 严 格(ge) 的 Burgers 位 向(xiang) 关(guan)系(xi)[9]。当冷(leng)却(que)速度较(jiao)慢时(shi),β-α 转(zhuan)变受到(dao)溶(rong)质元(yuan)素的(de)扩(kuo)散控制(zhi)��,两相(xiang)中(zhong)的(de)成分(fen)会有明显(xian)不(bu)同(tong)。除此(ci)以(yi)外(wai),当冷(leng)却(que)速度(du)很(hen)大时(shi)�,β 相转(zhuan)换(huan)成(cheng) α 相的(de)过程(cheng)可(ke)能来(lai)不及(ji)进(jin)行,此(ci)时(shi) β 相会发(fa)生(sheng)马氏(shi)体相变�,转变(bian)成(cheng)与(yu)母相成(cheng)分相(xiang)同��、晶(jing)体结构不同(tong)的过饱和(he)固溶(rong)体(ti)���,如(ru)六(liu)方马氏体 α'和斜(xie)方马(ma)氏体(ti) α''�����,此时(shi)相变(bian)过(guo)程(cheng)不(bu)发生元(yuan)素(su)扩(kuo)散(san)�����,主(zhu)要(yao)发生(sheng)晶(jing)格重(zhong)构(gou),转(zhuan)变也(ye)没有(you)孕育(yu)期���,相变动(dong)力学(xue)过(guo)程很(hen)快(kuai)�。从(cong)上面描(miao)述(shu)还(hai)可看出,钛合(he)金基(ji)体组织的相(xiang)变机制(zhi)与钢(gang)铁(tie)材(cai)料(liao)中(zhong)的奥(ao)氏体分(fen)解过程(cheng)比(bi)较(jiao)类似(shi)�����,也(ye)存(cun)在(zai)扩(kuo)散型和(he)切边型两(liang)种(zhong)类型(xing)的(de)相变。同时许(xu)多试验研究(jiu)均(jun)表明�����,β-α 的(de)扩(kuo)散(san)型(xing)相变也包(bao)含(han)孕育期���,相(xiang)变(bian)动(dong)力(li)学(xue)曲线也(ye)类似 S 型(xing)[10]。
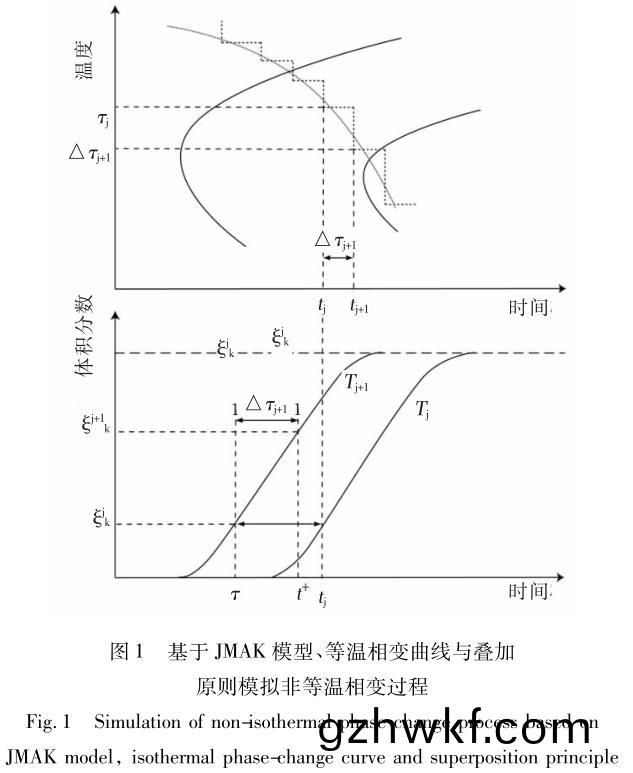
因(yin)此�,许多(duo)在钢铁(tie)材料(liao)中(zhong)的热(re)处理微观组(zu)织(zhi)计算(suan)方法也可(ke)用(yong)于钛合(he)金相变过程的计(ji)算(suan)�����。最(zui)经典(dian)描述(shu)扩散(san)型相(xiang)变的方程(cheng)是 Johnson-Mehl-Avrami-Kolmogorov( JMAK) 方程(cheng)[11 - 13]��,也被广(guang)泛应(ying)用(yong)于(yu)钛(tai)合(he)金的相(xiang)变动力(li)学(xue)模拟�。JMAK 方程是描(miao)述等(deng)温过(guo)程(cheng)的(de)相(xiang)变体积(ji)分 数(shu) 与(yu) 时 间(jian) 的 数(shu) 学 关(guan) 系(xi)��,通 过 Schlie 叠 加(jia) 原则(ze)[14 - 16]����,可将(jiang)非等(deng)温(wen)相(xiang)变(bian)过程(cheng)等价(jia)为多(duo)个微(wei)小等(deng)温(wen)过(guo)程的叠加(jia)�,从(cong)而实(shi)现任意温(wen)度下(xia)的微(wei)观(guan)组(zu)织(zhi)预(yu)测(ce),如(ru)图 1 所(suo)示[4]�����。通(tong)过(guo)对(dui)经(jing)典(dian) JMAK 方(fang)程的(de)修正与发(fa)展(zhan)��,可(ke)进(jin)一(yi)步在(zai)模型(xing)中(zhong)考虑(lv)初(chu)始母(mu)相(xiang)晶(jing)粒(li)度(du)的(de)影响(xiang)[17]。钛合金的(de) β 相(xiang)转(zhuan)变(bian)过(guo)程中(zhong)����,会(hui)形成多种形貌的(de) α 相组(zu)织��。针(zhen)对(dui)钛(tai)合金(jin)的这(zhe)种(zhong)特性(xing)�����,JMAK 方(fang)程(cheng)也被进(jin)一(yi)步(bu)发(fa)展(zhan)����,可(ke)用于(yu)预测等(deng)轴(zhou)晶、针状组织(zhi)等不(bu)同形(xing)貌 α 相(xiang)的(de)体(ti)积分数及其(qi)动(dong)力(li)学(xue)特(te)性(xing)�。Koistinen-Margurger( KM) 唯象模(mo)型(xing)及其变体形式被(bei)广泛(fan)应(ying)用于(yu)钢(gang)与(yu)钛(tai)合(he)金的马(ma)氏(shi)体(ti)切(qie)变(bian)型(xing)相(xiang)变[18 - 19]�。KM 模(mo)型比较(jiao)简(jian)洁(jie)�����,相(xiang)变分(fen)数与(yu)温度之(zhi)间(jian)的关系(xi)清(qing)晰明了���,相关参(can)数(shu)很容易确(que)定,在(zai)软(ruan)件二次(ci)开(kai)发中很容易(yi)实(shi)现(xian)�,但(dan)是(shi) KM 模型不(bu)能准(zhun)确(que)描述(shu)马氏体(ti)相(xiang)变(bian)初(chu)始阶段的(de)动力学。
Lusk 等根(gen)据(ju)连(lian)续冷(leng)却相变(bian)理论建立(li)了(le)针对扩散型相变(bian)与(yu)切变(bian)型相(xiang)变(bian)的(de)统(tong)一唯象模型(xing)[20],这(zhe)两类相变的体积(ji)分(fen)数(shu)和(he)温度(du)之(zhi)间(jian)的(de)关系可用(yong)公(gong)式( 1) 和(he)( 2) 表(biao)示(shi):
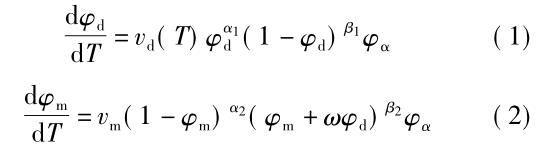
式(shi)中(zhong): φd 和 φm 表示扩(kuo)散相变(bian)和(he)切(qie)变相(xiang)变(bian)组(zu)织的(de)体(ti)积分(fen)数(shu); φα 表示母(mu)相(xiang)体(ti)积(ji)分数(shu); vd 和 vm 为相(xiang)变(bian)迁(qian)移率; α1�、α2����、β1����、β2 和(he) ω 为相(xiang)变动(dong)力(li)学(xue)参数。相关参数(shu)通过(guo)拟(ni)合(he) CCT 连续冷(leng)却相(xiang)变(bian)曲线获得�。
热(re)处理(li)过(guo)程中�����,与微观组织(zhi)相关的(de)力(li)学响应(ying)是(shi)另(ling)外(wai)一个重要的建模环节。由(you)于(yu)热(re)处理(li)过程的变形(xing)程度(du)较(jiao)小(xiao),为(wei)了准确描述其力学响应(ying)����,其本(ben)构模(mo)型(xing)中必须(xu)要(yao)包含弹(dan)性和(he)塑性,同时还要(yao)考虑(lv)卸(xie)载回弹的影(ying)响���。为(wei)了与微观(guan)组(zu)织(zhi)建(jian)立(li)关(guan)联,目前比较(jiao)合理的(de)热(re)处(chu)理(li)力学本(ben)构(gou)模(mo)型(xing)都是(shi)建立在单相的(de)基(ji)础上(shang),针对(dui)每(mei)一(yi)种相(xiang)变组织建(jian)立(li)力(li)学本(ben)构关(guan)系���,然后(hou)整个(ge)材料的力(li)学(xue)响(xiang)应(ying)通(tong)过非(fei)线(xian)性混(hun)合法则来确定(ding)[1]���。近年来�,Bammann、Chiesa 和(he) Johnson 等(deng)从(cong)位错(cuo)理论出发�����,提出(chu)一种(zhong)基(ji)于内(nei)变量的(de)力学本构(gou)模(mo)型,这一(yi)模(mo)型最初主要(yao)用于(yu)塑(su)性(xing)变形(xing)和切(qie)削(xue)加工(gong)等工艺(yi)领(ling)域(yu)。近年来����,Bammann-Chiesa-Johnson 本构模(mo)型也被用(yong)于热处理(li)仿(fang)真(zhen)�����,来描述(shu)每一种(zhong)相的本构关(guan)系[21 - 24]�����。相(xiang)比(bi)传(chuan)统(tong)的(de)热(re)弹(dan)塑性(xing)模型(xing),BCJ 模型不仅可以准(zhun)确模拟回(hui)弹(dan)等(deng)因素对(dui)变(bian)形(xing)的影(ying)响���,还(hai)可(ke)以(yi)实现(xian)和(he)应变速(su)率(lv)相关(guan)的(de)力(li)学响(xiang)应(ying)预测,在(zai)较大(da)的温(wen)度区间(jian)和较(jiao)大(da)的变形(xing)速(su)率(lv)范(fan)围内���,都有(you)很高的模(mo)拟精(jing)度。根据(ju) BCJ 模型����,每一个(ge)相(xiang)的屈服(fu)判据(ju)可以用如下(xia)公(gong)式描(miao)述(shu):
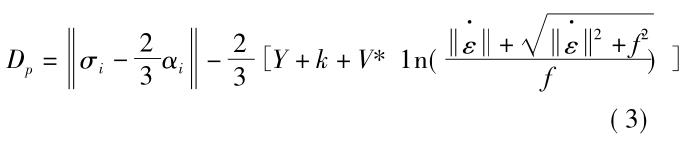
当 Dp≥0 时(shi)���,对(dui)应相进(jin)入屈(qu)服状态�,否(fou)则(ze)仍处(chu)于弹性状态。在(zai)公(gong)式(shi)( 3) 中�����,α 为(wei)张量内(nei)变量����,k 为标量(liang)内变量(liang),σ 为(wei)偏(pian)应力(li)张(zhang)量(liang)����,Y 为率无关(guan)函(han)数,V 和(he) f 为率相(xiang)关函(han)数�。上(shang)述参数(shu)可以通(tong)过不(bu)同温(wen)度(du)下的(de)单轴(zhou)拉伸(shen)或压缩(suo)应(ying)力-应变曲(qu)线拟合(he)获得。
在热处(chu)理(li)过程(cheng)中�����,也必须(xu)考虑(lv)应(ying)力(li)与相变的交互作(zuo)用�,其(qi)中一(yi)个重要的(de)现象(xiang)就是相变塑(su)性����。相(xiang)变组(zu)织由(you)于(yu)晶(jing)格(ge)参数(shu)的不同(tong),往(wang)往会发(fa)生体积变化����。
最典(dian)型的(de)是在(zai)马氏体相(xiang)变(bian)过程(cheng)中,会发生体(ti)积膨(peng)胀(zhang)。这种膨(peng)胀(zhang)会导(dao)致新相(xiang)与(yu)母相(xiang)之间(jian)发(fa)生相(xiang)变诱(you)导塑(su)性(xing)现(xian)象(xiang)���,也就(jiu)是在外加应力(li)远(yuan)远(yuan)低(di)于屈服(fu)应(ying)力状态(tai)时发(fa)生(sheng)的(de)塑性变(bian)形(xing)。对整个(ge)变(bian)形影(ying)响较大(da),在(zai)实际(ji)过程中(zhong)不(bu)可(ke)忽略�。Greenwood 和 Johnson 建(jian)立(li)了(le)一(yi)个数学模(mo)型(xing)来(lai)描述(shu)这(zhe)种相(xiang)变(bian)过(guo)程中(zhong)由(you)于(yu)蠕(ru)变导(dao)致(zhi)的塑性(xing)变形(xing)����,在钢(gang)铁材(cai)料的(de)热处(chu)理仿真中(zhong)得(de)到(dao)了(le)广泛应(ying)用(yong)�����。相(xiang)变(bian)塑性效(xiao)应模型采(cai)用如(ru)下(xia)公(gong)式描述[25 - 26]:
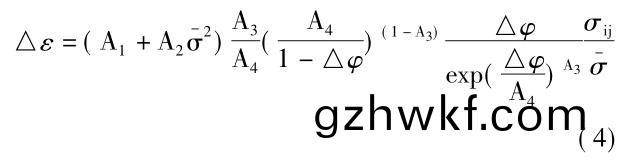
式(shi)中(zhong): △ε 为(wei)相(xiang)变诱导塑性(xing)应(ying)变; σ 为等(deng)效应(ying)力(li); σij为偏应(ying)力(li)张(zhang)量(liang); △φ 为(wei)相变(bian)组(zu)织(zhi)体(ti)积(ji)分数; A2 为(wei)常数���,可(ke)通(tong)过拟(ni)合(he)伴(ban)随(sui)相(xiang)变的(de)拉(la)伸或(huo)压(ya)缩应变(bian)-应变曲(qu)线获(huo)得���。这(zhe)一(yi)模(mo)型在(zai)钢铁材料(liao)的(de)相(xiang)变(bian)中得到(dao)的广泛应(ying)用���,最近 Schuh 等人针对(dui)钛合金的相变(bian)超(chao)塑(su)性���,发展了这一(yi)模(mo)型(xing),将其(qi)扩(kuo)展至非等(deng)温(wen)的(de)相(xiang)变过程��,并(bing)采用Ti-6Al-4V 合金的(de)热(re)循环(huan)试验对这一(yi)模型(xing)进(jin)行(xing)了(le)验(yan)证[27]���。
2�、热(re)处理仿(fang)真(zhen)在钛合金(jin)中的(de)应(ying)用(yong)
达(da)索公(gong)司的(de) Zhang 和 Chin 等以(yi)增材(cai)制(zhi)造工(gong)艺(yi)为(wei)研究(jiu)对(dui)象(xiang)[28 - 29],针对(dui)钛(tai)合(he)金增(zeng)材制(zhi)造冷却与热(re)处理过程����,构建出相(xiang)变(bian)模(mo)拟框架,采(cai)用 KM 方(fang)程模拟快速(su)冷(leng)却(que)过程(cheng)的(de) β-α'马氏体相(xiang)变(bian),JMAK 方程模拟(ni)钛(tai)合金(jin)的 β-α 扩(kuo)散(san)型(xing)相(xiang)变(bian)动(dong)力学(xue),模型中(zhong)考虑了(le) β 相的(de)初(chu)始(shi)晶粒尺寸对相变(bian)动力(li)学的影(ying)响,也可(ke)以进(jin)一(yi)步模(mo)拟(ni) α' 相 的(de) 板 条 束 宽(kuan) 度(du)[29]。基(ji) 于(yu) 这(zhe) 一(yi) 框 架(jia)���,在ABAQUS 中(zhong)进行(xing)二(er)次(ci)开发(fa),成(cheng)功预测了 TC4 钛(tai)合(he)金在(zai)增(zeng)材制(zhi)造(zao)过程(cheng)中(zhong)所得(de)到的(de)微(wei)观(guan)组织(zhi)( 图 2) ,模拟结(jie)果与扫描(miao)电镜(jing)的(de)试验结(jie)果(guo)吻(wen)合很(hen)好(hao)。

Semiatin 等(deng)构建(jian)出(chu)基于(yu)平(ping)均(jun)场(chang)理论的相(xiang)变(bian)模型[30],可(ke)模拟任意(yi)冷却路(lu)径(jing)下(xia)的(de)初生 α 相(xiang)晶(jing)粒(li)尺(chi)寸和(he)体(ti)积(ji)分数(shu)����,也可扩展用于 TC4 和 Ti6242 合(he)金(jin)中(zhong)的双态(tai)组(zu)织预(yu)测。将此(ci)模(mo)型(xing)和 DEFORM 有(you)限元软(ruan)件结(jie)合(he),有限(xian)元(yuan)模(mo)拟(ni)得到的零(ling)件局(ju)部位置(zhi)冷却路径作(zuo)为输(shu)入条件,从而(er)可(ke)模(mo)拟整(zheng)个零(ling)件截(jie)面(mian)的微观组(zu)织。
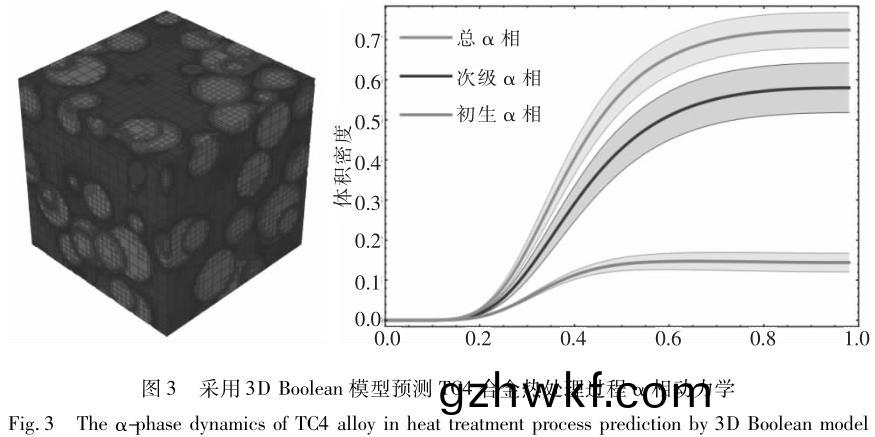
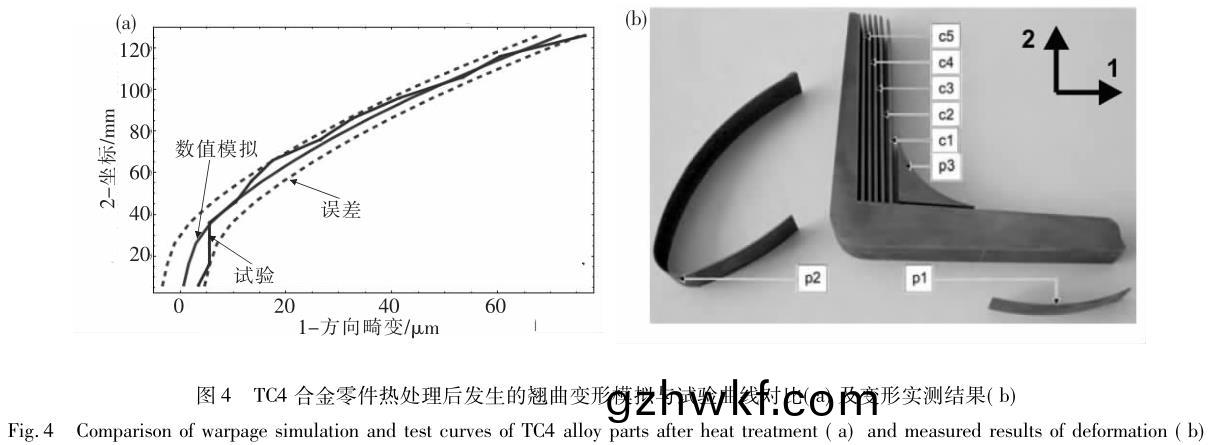
Regner 等采(cai)用 Johnson-Mehl tessellation 和(he) Boolean 模(mo)型模拟 TC4 合金锻(duan)造与(yu)热(re)处(chu)理过(guo)程(cheng)初(chu)生 α 相(xiang)的形(xing)成(cheng)[31]��,这(zhe)一模(mo)型同样(yang)基于平(ping)均(jun)场理论���,可(ke)以与(yu)宏(hong)观温(wen)度(du)场、变(bian)形场(chang)相(xiang)互(hu)耦合计(ji)算求解,如(ru)图 3 与图(tu) 4 所(suo)示�����。Teixeira 等(deng)提出(chu)一(yi)个(ge)相变模(mo)型预测(ce)近(jin) β 钛合(he)金在冷却(que)过(guo)程中(zhong)的相变(bian)动(dong)力学(xue)[32 - 33]�����。采用(yong) JMAK 模型计算(suan)晶内(nei)魏(wei)氏(shi)组织(zhi)的相(xiang)变动力(li)学(xue)���,采(cai)用形(xing)核-长大(da)的平均场扩散理(li)论(lun)模拟(ni)晶界(jie) α 相和(he)魏(wei)氏组织的(de)动力(li)学(xue)与(yu)形貌(mao)。该模(mo)型(xing)也(ye)可(ke)考(kao)虑因(yin) β 相变(bian)形(xing)所带来的(de) β相(xiang)晶(jing)粒(li)尺寸及(ji)亚晶(jing)对相(xiang)变(bian)的(de)影(ying)响(xiang)。此模型在(zai) Ti17 合金(jin)和 β-Cez 合(he)金中应用(yong)����,成(cheng)功地预测(ce)了不同(tong)形态(tai) α相的体(ti)积(ji)分数及(ji)其分(fen)布��。Malinov 和(he) Sha 等(deng)通过 DSC试验(yan)曲线(xian)推(tui)导(dao)出(chu) JMAK 方程(cheng)参数,用于模(mo)拟(ni) β-α 相(xiang)变后(hou)��,α 晶(jing)粒的分数(shu)以(yi)及形貌[36]。
Schuh 等针对在(zai)外(wai)加应(ying)力条件下(xia)的(de)钛合金相(xiang)变超(chao)塑(su)性(xing)现(xian)象(xiang)提出了一(yi)个(ge)数学(xue)模(mo)型(xing)��,研究(jiu)表明(ming)该(gai)模(mo)型可(ke)准确(que)模(mo)拟(ni)加热(re)与冷(leng)却循环(huan)过程(cheng)中(zhong)产生的(de)应变(bian)增量(liang)。结(jie)合(he) JMAK 方程(cheng),就(jiu)可以建立一(yi)个(ge)耦合模型(xing),描述(shu)温度(du)-应(ying)力-相(xiang)变之(zhi)间(jian)的交(jiao)互作用(yong)[27]。Malinov 等建立了(le)神(shen)经网(wang)络(luo)模型来模(mo)拟(ni)成(cheng)分与(yu)工艺(yi)对钛合金(jin)微观组(zu)织及(ji)力学(xue)性(xing)能(neng)的影响(xiang)[34 - 35]�。由(you)于神(shen)经(jing)网(wang)络模型属于黑(hei)箱算法(fa)��,不(bu)涉(she)及任何物理机(ji)制与(yu)建模(mo)���,主要(yao)通过大量(liang)实验(yan)数据(ju)建(jian)立(li)工(gong)艺参(can)数(shu)、成分(fen)与(yu)微(wei)观组(zu)织�、力(li)学(xue)性(xing)能之间的关(guan)系(xi)���。该(gai)模型最终(zhong)决定的(de)是(shi)微(wei)观组织分(fen)数以(yi)及(ji)对力学(xue)性(xing)能的影响��,无(wu)法(fa)对(dui)应力(li)及(ji)翘(qiao)曲变(bian)形(xing)进(jin)行(xing)仿真(zhen)模(mo)拟(ni)�。Krafft 等(deng)采(cai)用(yong)有限元(yuan)软(ruan)件 Forge构建钛(tai)合(he)金热(re)处理(li)过程的相(xiang)变动(dong)力学计(ji)算模(mo)型���。该(gai)模(mo)型(xing)不仅可(ke)实(shi)现(xian) β 相(xiang)和 α 相分数(shu)的预测(ce),还(hai)可(ke)预测(ce)α 相的(de)不(bu)同(tong)形貌及其占比。另外�,此模型(xing)也(ye)常被(bei)用于(yu) Ti17 和(he) Ti-6Al-4V 合(he)金(jin)航(hang)空发(fa)动(dong)机压气机(ji)盘均(jun)匀(yun)化、锻造(zao)����、退(tui)火(huo)的加(jia)工(gong)全过程[37]���。
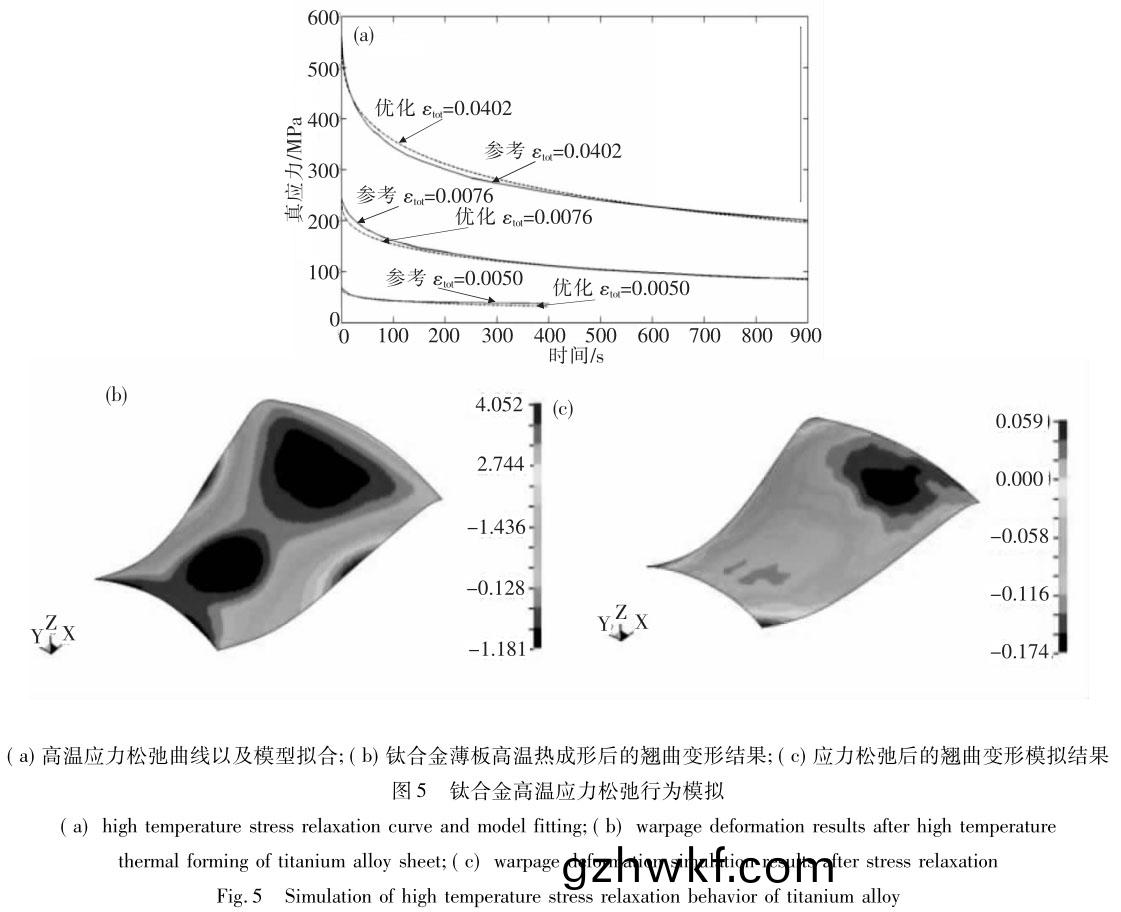
Odenberger 等采用(yong) Zener-Wert-Avrami 模(mo)型描述(shu)钛(tai)合(he)金的(de)高(gao)温应(ying)力(li)松弛(chi)行(xing)为(wei),如图(tu) 5 所示[38]����。王伟等(deng)基于(yu)经(jing)典(dian) Norton 公式(shi)建(jian)立(li) Ti-6Al-4V 合金热粘(zhan)塑(su)性本构模(mo)型(xing)[39�����,43],在对初始残(can)余(yu)应(ying)力做(zuo)假(jia)设(she)和简(jian)化(hua)基础上�,分析钛合金(jin)薄板不同(tong)退(tui)火(huo)温(wen)度(du)对(dui)退(tui)火(huo)变形(xing)的(de)影响规(gui)律(lv)�����,并(bing)结(jie)合试验(yan)验证(zheng)模(mo)拟结果(guo)。刘向(xiang)前等(deng)采(cai)用有限(xian)元(yuan)法研究 TC4 薄(bao)壁圆筒件(jian)热旋(xuan)压后(hou)的(de)冷却温(wen)度(du)场分布(bu)及(ji)冷(leng)却后残余应力与变(bian)形(xing)情(qing)况(kuang),在此基(ji)础上���,考(kao)虑(lv)旋压过程的(de)残(can)余应力(li),使(shi)用蠕变(bian)材(cai)料模型(xing)计算(suan)薄(bao)壁(bi)圆(yuan)筒件去(qu)应力退火(huo)的(de)变(bian)形(xing)情况(kuang)[41]����。由(you)于(yu)
热(re)旋压(ya)温(wen)度(du)以及(ji)退火温度(du)并(bing)未(wei)超过(guo) β 相变点,因(yin)此在(zai)模拟过(guo)程中不用考(kao)虑基体相变的(de)作用��,主要考虑弹塑(su)性(xing)以及蠕(ru)变塑(su)性变(bian)形�����。王明伟(wei)等研究钛合金(jin)真空热(re)处理及热胀(zhang)形过程(cheng)数值模拟[42],预测(ce)出加热过程(cheng)的(de)滞(zhi)后时间(jian),并(bing)建立(li) BT20 钛(tai)合金筒(tong)形(xing)件(jian)真(zhen)空热(re)胀过(guo)程(cheng)的热(re)力耦(ou)合有(you)限元模型�,得到(dao)可(ke)用于(yu)工业生产的工艺参(can)数(shu)方(fang)案(an)。陈(chen)涛等建立了(le) TC18 钛(tai)合金(jin)退火态(tai)应(ying)力(li)松弛行(xing)为的(de)本构关系(xi)[40],并用于长(zhang)直(zhi)杆(gan)件焊(han)后退火热(re)处(chu)理(li)过程的(de)模拟(ni),研(yan)究(jiu)了(le)退火加(jia)热(re)与冷(leng)却过程(cheng)的(de)残(can)余应力(li)与(yu)变(bian)形规律�����,结(jie)果为(wei)变形控制以及(ji)后续的热校形(xing)工(gong)艺提(ti)供(gong)了(le)指导依据��。Alberg 等采用(yong)数值模拟(ni)的(de)方(fang)法研(yan)究(jiu)了航(hang)空(kong)发动机零部件焊接及(ji)焊后热(re)处理(li)过(guo)程的畸变变形问题(ti)[44]。
3、总结(jie)与展(zhan)望(wang)
近(jin)三十年来(lai)��,钛(tai)合金热(re)处(chu)理工艺(yi)仿真(zhen)的(de)基(ji)础(chu)理论(lun)�����、数值(zhi)模型与(yu)工(gong)程(cheng)应(ying)用得到了(le)长(zhang)足发展�,在微观组织(zhi)分布、残余(yu)应(ying)力(li)与(yu)翘曲变(bian)形(xing)预(yu)测(ce)等(deng)方(fang)面(mian)得(de)到广泛应(ying)用(yong)�。目(mu)前,在热(re)处理(li)工(gong)艺(yi)中,引(yin)入(ru)计(ji)算机模(mo)拟(ni)已成为加(jia)工制(zhi)造(zao)业的(de)发展(zhan)趋(qu)势(shi)�,人(ren)们对材料(liao)热(re)处理过(guo)程(cheng)采用(yong)计算机模拟(ni)重要性和(he)意义(yi)的(de)认(ren)识在不断(duan)加(jia)深。
钛合(he)金(jin)热处(chu)理(li)过(guo)程的数(shu)值模拟(ni)虽已(yi)取得(de)一(yi)定(ding)进(jin)展(zhan)�,但(dan)仍(reng)然(ran)面临许多挑战(zhan)�。例如�����,热(re)处(chu)理(li)过程(cheng)涉(she)及(ji)到的外部因(yin)素复杂����,除(chu)模(mo)型(xing)和(he)算法(fa)的(de)可(ke)靠性(xing)外,材料及介(jie)质参(can)数(shu)的准确(que)性(xing)也是非常关键的(de)环(huan)节���。这(zhe)些(xie)参数(shu)包(bao)括(kuo)热物(wu)性(xing)参(can)数(shu)( 导热系(xi)数、热容�����、热膨胀(zhang)系数、相变(bian)潜(qian)热(re)) �、力(li)学(xue)性(xing)能参(can)数( 弹(dan)性(xing)模量���、泊(po)松比(bi)、屈服(fu)强(qiang)度�、塑(su)性模量) �����、相变(bian)动(dong)力(li)学参(can)数(shu)、相(xiang)变(bian)膨胀(zhang)系数�、相(xiang)变(bian)塑(su)性(xing)系数(shu)和(he)淬火过(guo)程中(zhong)的(de)工(gong)件(jian)表(biao)面(mian)各处(chu)的换热系数等[3]�。以界面换(huan)热(re)系数为(wei)例(li),这一(yi)参数是(shi)决定工件(jian)温(wen)度(du)场分(fen)布(bu)的(de)核(he)心(xin)参(can)数,与(yu)介(jie)质、工(gong)件以(yi)及实际(ji)的工艺(yi)实施方(fang)案(an)密(mi)切相关。因(yin)此(ci)在(zai)实际(ji)热处(chu)理(li)仿(fang)真(zhen)中(zhong),必(bi)须(xu)要(yao)结(jie)合现(xian)场实(shi)际(ji)条(tiao)件(jian)进(jin)行测(ce)量和(he)反(fan)求(qiu),才能(neng)让模拟结果(guo)接(jie)近实际情况(kuang)�。此(ci)外(wai)�,热(re)处(chu)理(li)残余(yu)应(ying)力(li)和变(bian)形的高精度(du)仿(fang)真仍(reng)然(ran)是一(yi)个难(nan)点�����,一方(fang)面残(can)余应(ying)力很(hen)难通过试(shi)验进行准确(que)验(yan)证(zheng)和校核(he)�,需要(yao)发展(zhan)先进的(de)残余(yu)应力(li)试(shi)验技(ji)术(shu)对(dui)相(xiang)关(guan)模型和算法(fa)进(jin)行验(yan)证(zheng); 另一方面(mian)热(re)处理(li)变(bian)形(xing)涉及(ji)到的(de)温度(du)范(fan)围(wei)宽��,影(ying)响(xiang)因(yin)素(su)较(jiao)多,对材料的本构(gou)模(mo)型(xing)与计(ji)算(suan)精(jing)度提(ti)出(chu)很(hen)高(gao)要(yao)求(qiu),需(xu)要(yao)进(jin)一(yi)步(bu)进行(xing)深入(ru)研究[1]����。
近(jin)年(nian)来�,基(ji)于(yu)介观尺(chi)度(du)的微观组(zu)织演(yan)化计算方法(fa)也(ye)得(de)到了(le)很大(da)的发展(zhan)���。以(yi)相(xiang)场方(fang)法(fa)为代(dai)表(biao)的(de)介(jie)观(guan)计算方法(fa)可(ke)从(cong)机理(li)上(shang)模拟(ni)钛合金(jin)热(re)处(chu)理(li)过(guo)程(cheng)发(fa)生的(de)相变(bian)[45 - 49],不(bu)再(zai)局限(xian)于 JMAK 模(mo)型(xing)等平均场理论(lun),可(ke)从(cong)单(dan)个晶粒(li)的层次来(lai)模拟微观组(zu)织(zhi)演化����,不(bu)仅(jin)可预(yu)测相变(bian)组(zu)织及(ji)其体(ti)积(ji)分数,还(hai)可(ke)预(yu)测(ce)组(zu)织形(xing)貌、溶质元(yuan)素(su)分(fen)布(bu)甚至新(xin)相(xiang)变(bian)体(ti)取(qu)向规(gui)律���。未(wei)来随着(zhe)计算机能(neng)力的增(zeng)强以(yi)及算(suan)法的发(fa)展(zhan),有望(wang)将(jiang)介观(guan)尺度(du)微(wei)观组(zu)织(zhi)演(yan)化(hua)计算方(fang)法(fa)与(yu)宏(hong)观的温度场(chang)以(yi)及应(ying)力/应变场进(jin)行(xing)耦合计算(suan),从而(er)使(shi)热(re)处(chu)理工(gong)艺仿真(zhen)向(xiang)多尺(chi)度方向(xiang)发展�,使材(cai)料设计(ji)与(yu)零部(bu)件(jian)制(zhi)备(bei)有(you)效(xiao)结(jie)合(he)起(qi)来(lai)。未(wei)来(lai)随(sui)着(zhe)基(ji)础理(li)论(lun)����、模(mo)型(xing)和材(cai)料(liao)数据(ju)库(ku)的不(bu)断完善(shan),热(re)处理(li)技(ji)术(shu)终(zhong)将摆(bai)脱凭经验依赖,向精确(que)预测���、定量控制(zhi)和(he)设计(ji)制(zhi)造一体化(hua)与(yu)智能化(hua)的(de)方向飞(fei)跃(yue)����。
参(can)考文献
[1] Gur C H���,Pan J S. Handbook of thermal process modeling of steels[M]. CRS Press����,2009.
[2] 潘(pan)健生(sheng),张伟(wei)民(min),田(tian)东,等. 热(re)处(chu)理数学(xue)模型(xing)与计(ji)算机模拟[J]. 中(zhong)国(guo)工程(cheng)科学(xue)���,2003( 5) : 47 - 54.
[3]Denis S��,Sjostrom S,Simon A.Coupled temperature,stress�����,phase transformation calculation[J]. MetallurgicalTransactions A���,1987( 18) : 1203 - 1212.
[4]SiMSiR C�����,Cemil Hakan GUR. A Mathematical Frame-work for Simulation of Thermal Processing of Materials [J]. Application to Steel Quenching. Turkish Journal ofEngineering & Enviromental Sicence��,2008 ( 32) : 85 -100.
[5]刘庄,吴肇基(ji),吴景(jing)之(zhi)�,等(deng). 热处理过程的(de)数(shu)值(zhi)模拟(ni)[M]. 北(bei)京: 科(ke)学(xue)出(chu)版(ban)社,1996.
[6] Pan J S ,Li Y J����,Gu J F,et al. Research and application of computer on heat treatment process[J]. Journal of Shanghai Jiao Tong University ,2000E( 5) : 1 - 13.
[7]Inoue T ����,Wang Z G. Coupling between stress,tempera-ture and metallic structures during processes involvingphase transformations[J]. Materials Science and Technolo-gy,1985( 10) : 845 - 850�,
[8]Inoue T ,Funatani K,Totten G E. Process modeling for heat treatment:current status and future developments[J]. Journal of Shanghai Jiao Tong University,2000E( 5) : 14 - 25.
[9]赵永庆(qing),陈(chen)永(yong)楠(nan),张(zhang)学敏(min),等. 钛(tai)合金相变(bian)及(ji)热处(chu)理(li)[M]. 长沙(sha): 中(zhong)南大学出(chu)版社(she),2012.
[10] Elmer J W���,Palmer T A,Babu S S,et al. In situ observa-tions of lattice expansion and transformation rates of α andβ phases in Ti-6Al-4V[J]. Materials Science and Engi-neering: A 2005,391: 104 - 113.
[11] Johnson W A�����,Mehl R F. Reaction kinetics in processes of nucleation and growth transaction[J]. AIME,1939( 135) : 396 - 415.
[12] Avrami M. Granulation���,phase change,and microstruc-ture kinetics of phase change III[J].The Journal of Chemical Physics,1941( 9) : 177 - 184.
[13] Avrami M. Kinetics of phase change. I. General theory[J]. The Journal of Chemical Physics�����,1939( 7) : 1103 -1112.
[14] Réti T,Felde I. A non-linear extension of the additivity rule[J]. Computational Materials Science,1999 ( 15) :466 - 482.
[15] Ye J S���,Hsu T Y. Modification of the additivity hypothesis with experiment[J]. ISIJ International,2004( 44) : 777 -779.
[16] Hsu T Y. Additivity hypothesis and effects of stress on phase transformations in steel[J]. Current Opinion in Sol-id State and Materials Science,2005( 9) : 256 - 268.
[17] Hawbolt E,Chau B��,Brimacombe J. Kinetics of austenite-pearlite transformation in eutectoid carbon steel[J]. Metal-lurgical Transactions A,1983( 14) : 1803 - 1815.
[18] Lee S J,Lee Y K. Finite element simulation of quench distortion in a low-alloy steel incorporating transformation dinetics[J]. Acta Materialia,2008( 56) : 1482 - 1490.
[19] Koistinen D P,Marburger R E. A general equation pre-scribing the extent of the austenite-martensite transforma-tion in pure iron-carbon alloys and plain carbon steels[J].Acta Metallurgica,1959( 7) : 59 - 60.
[20] Lusk M T,Lee Y K,Jou H J ,et al. An international state variable model for the low temperature tempering of low alloy steels[J]. Journal of Shanghai Jiao Tong Univer-sity,2000E( 5) : 178 - 184.
[21] Bammann D,Hou H J. Development of a carburizing and quenching simulation Tool: A material model for steels un-dergoing phase transformations[A]. Proceeding of the sec-ond international conference on quenching and the control of distortion[C]. Cleveland,Ohio�,1996.
[22] Johnson G C����,Bammann D J. Discussion of stress rates in finite deformation problems[J]. International Solids Struc-ture����,1984( 20) : 725 - 736.
[23] Bammann D J. An internal variable model of viscoplastici-ty[J]. International Journal of Engineering Science�����,1984( 22) : 1041 - 1051.
[24] Li Z C����,Ferguson B L. Effect of quenching rate on distor-tion and residual stresses during induction hardening of a full-float truck axle shaft[J]. Journal of Materials Engi-neering and Performance,2014( 23) : 4170 - 4180.
[25] Greenwood G W,Johnson R H. The deformation of metals under small stresses during phase transformations[J]. Pro-ceedings of the Royal Society A: Mathematical���,Physical and Engineering Sciences�����,1965,283: 403 - 422.
[26] Leblond J B ,Devaux J. Mathematical modeling of trans-formation plasticity in steels I: Case of ideal-plastic phases[J]. International Journal of Plasticity�����,1989( 5) : 551 -572.
[27] Schuh C,Dunand D C. Non-isothermal transformation-mismatch plasticity: modeling and experiments on Ti-6Al-4V[J]. Acta Materialia����,2001( 49) : 199 - 210.
[28] Zhang Q,Xie J�,Gao Z�,et al. A metallurgical phase transformation framework applied to SLM additive manu-facturing processes[J]. Materials & Design,2019,166:107618.
[29] Chin C. Additive manufacturing process simulation valida-tions and microstructure prediction[J].
[30] Semiatin S L,Knisley S L��,Fagin P N,et al. Microstruc-ture evolution during alpha-beta heat treatment of Ti-6Al-4V[J]. Metall and Mat Trans A,2003���,34: 2377 - 2386.
[31] Regener�,Krempaszky B C�,Stockinger E W M. Innova-tive forging and heat treatment simulation of titanium alloys [A]. VPE Swiss Symposium����,2013.
[32] Teixeira D�����,Julien��,Appolaire B����,et al. Modeling of the phase transformations in near-β titanium alloys during the cooling after forging[J]. Computational Materials Science 2008,42: 266 - 280.
[33] Julien R,Velay V.Characterization and modeling of forged Ti-6Al-4V titanium alloy with microstructural con-siderations during quenching process [J]. International Journal of Mechanical Sciences�����,2018( 142 /143) : 456 -467.
[34] Malinov S,Sha W. The neural network modeling of titani-um alloy phase transformation and mechanical properties [J]. JOM�,2005�����,57: 54 - 57.
[35] Malinov S,Sha W. Modelling the correlation between pro-cessing parameters and properties in titanium alloys using artificial neural network[J]. Computational Materials Sci-ence,2001���,21: 375 - 394.
[36] Malinov S,Sha W. Modeling thermodynamics,kinetics,and phase transformation morphology while heat treating ti-tanium alloys[J]. JOM,2005,57: 42 - 45.
[37] Krafft O,Settefrati A��,Lasne P. The newest benefits of sim-ulation for heat treatment & microstructure prediction[DB/OA]. http: / /www. transvalor. com/uploaded/ckeditor/files/Articles/FORGE/.
[38] Odenberger E. Virtual process chain for superalloy & tita-nium sheet metal aero engine structures validation and demonstrators[A]. Third International Workshop on Vali-dation of Computational Mechanics Models[C].
[39] 王伟(wei),徐(xu)建军,李华冠,等. 退(tui)火温(wen)度对(dui) Ti6A14V 薄板(ban)退(tui)火(huo)变(bian)形(xing)影(ying)响(xiang)的(de)有限(xian)元(yuan)分(fen)析及(ji)实(shi)验验证[J]. 南京航(hang)空(kong)航(hang)天(tian)大学学报�����,2015,47( 5) : 737 - 744.
[40] 陈涛. TC18 钛合(he)金(jin)热(re)变(bian)形行为与(yu)热(re)处理数(shu)值模(mo)拟[D]. 哈尔滨: 哈(ha)尔滨(bin)工(gong)业大(da)学,2013.
[41] 刘向前(qian). TC4 钛(tai)合金薄(bao)壁圆筒(tong)件热成形后冷却热(re)应力(li)及(ji)变(bian)形模拟[D]. 哈尔(er)滨: 哈尔(er)滨工(gong)业大学���,2005.
[42] 王(wang)明伟(wei). 高(gao)温合金和(he)钛合金真(zhen)空热处理及(ji)热胀形过程数(shu)值模(mo)拟[D]. 大连(lian): 大(da)连(lian)理(li)工大(da)学���,2007.
[43] 王(wang)伟(wei)�,徐建(jian)军(jun)���,杨吟(yin)飞,等. Ti6Al4V 钛(tai)合金(jin)薄板退火(huo)畸(ji)变(bian)数值模(mo)拟及试(shi)验(yan)验证(zheng)[J]. 金属热处理,2016�,41( 1) : 204 - 210.
[44] Henrik Alberg. Simulation of welding and heat treatment modelling and validation [D]. Lulea�����。�,Sweden: Lulea���。U-niversity of Technology����,2005.
[45] Chen Q,Ma N�,Wang Y. Quantitative phase field model-ing of diffusion-controlled precipitate growth and dissolu-tion in Ti-Al-V[J]. Scripta Materialia��,2004�����,50: 471 -476.
[46] Steinbach I. Phase-field models in materials science[J].Modelling and Simulation in Materials Science and Engi-neering,2009,17: 073001.
[47] Qiu D�����,Shi R�����,Zhang D���,et al. Variant selection by dislo-cations during α precipitation in α/β titanium alloys[J].Acta Materialia�����,2015,88: 218 - 231.
[48] Glavicic M G,Venkatesh V. Integrated computational ma-terials engineering of titanium: current capabilities being developed under the metals affordability initiative[J].JOM����,2014��,66: 1310 - 1320.
[49] Jou H J,Lusk M T. . Comparison of Johnson-Meh1-Avra-mi-Kologoromov kinetics with a phase-field model for mi-crostructural evolution driven by substructure energy[J].Physical Review B �����,1997,55 ( 13) : 8114 - 8121.
相(xiang)关链接